What is OpenBTS?

OpenBTS is a Unix application that uses a software radio to present a GSM air interface to standard 2G GSM handset and uses a SIP softswitch or PBX to connect calls. (You might even say that OpenBTS is a simplified form of IMS that works with 2G feature-phone handsets.) The combination of the global-standard GSM air interface with low-cost VoIP backhaul forms the basis of a new type of cellular network that can be deployed and operated at substantially lower cost than existing technologies in many applications, including rural cellular deployments and private cellular networks in remote areas.

Where can I get the latest code?

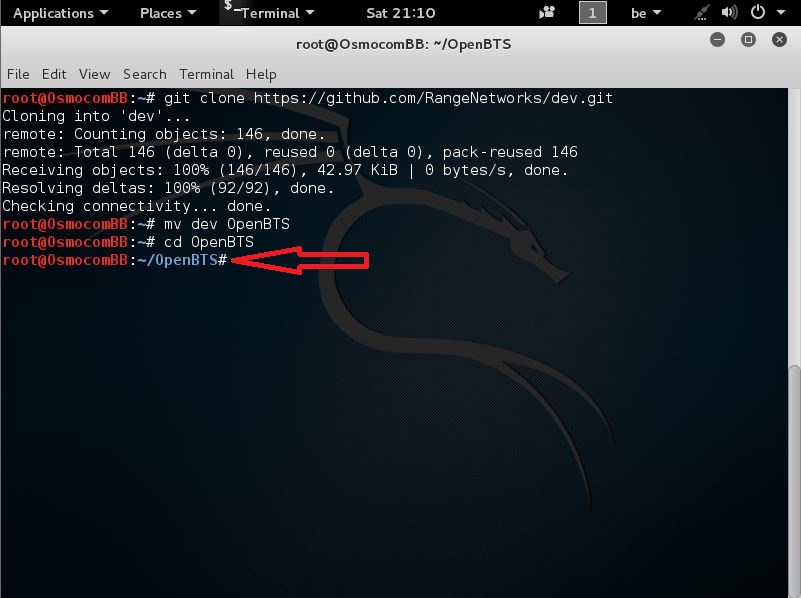
The best way to get OpenBTS is by pulling the code directly from there source code repository as an anonymous read-only user.

You do this by entering the following command into a new terminal window

git clone https://github.com/RangeNetworks/dev.git

like seen here

when u have entered that command

u can press Enter

and next u will see this

now that this i done we are going to change that Directory name into OpenBTS so u can remember it easily

to do that u need to enter the following command:

 mv dev OpenBTS

like seen here

when u typed this command u can press Enter

So now we renamed the folder dev to OpenBTS

Next we need to enter that directory, you do this by entering the following command:

cd OpenBTS

like seen here

after thats done press Enter

and you should now be here

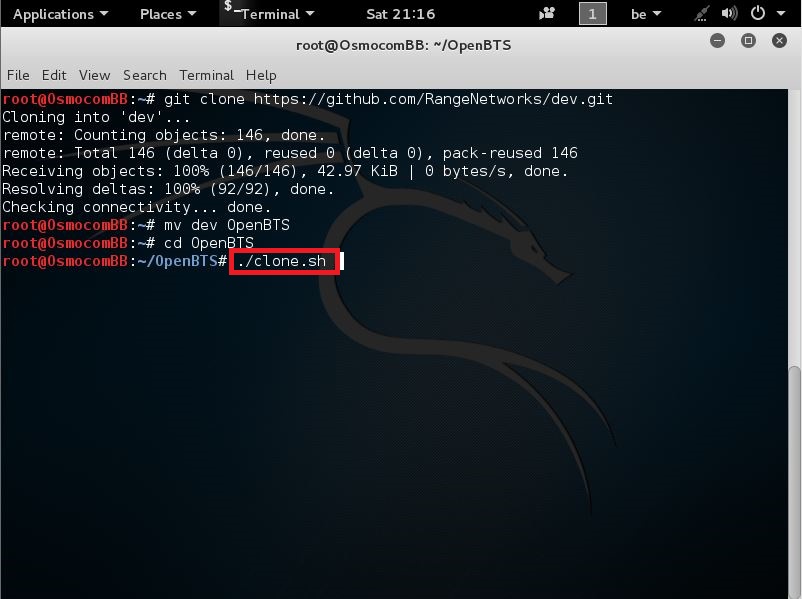
Now, to download all of the components simply run the clone.sh script.

u do this entering the following command

./clone.sh

like seen here

after that u can press Enter

 

Now if u pressed enter it’s going to pull all the needed software from the github

Component	master status
asterisk
asterisk-config
liba53
libcoredumper
libsqliteodbc
libzmq
openbts
smqueue
subscriberRegistry
system-config

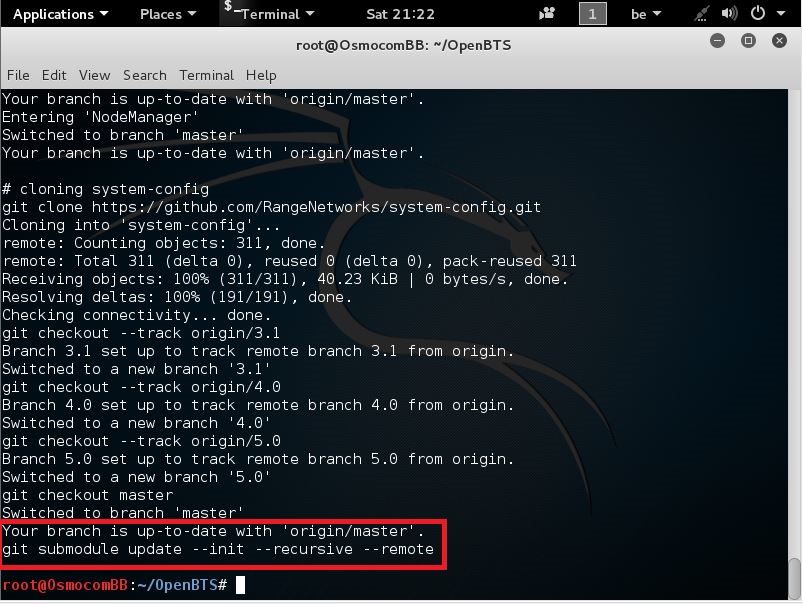
it’s a whole list, so i am not going to post the whole list in screenshots, but it should end with this

now that this is done we need to build it

Building

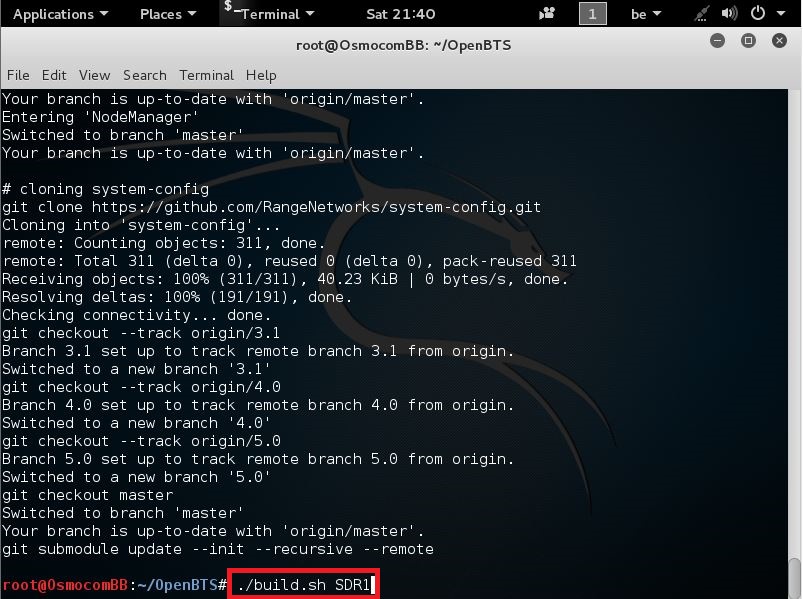
The build.sh script will automatically install any build dependencies (building them manually when required).

After dependencies are taken care of, each component is compiled into an installable package.

To do this we need to enter the following command:

./build.sh SDR1

like seen here

after u entered that command press Enter

This is a very long process, so go grab yourself a drink and lay back

After a while when it’s done

you should see this

Now the building is done !

Next we need to configure all the things

Configuring OpenBTS

With OpenBTS built, you now need to configure it to run correctly. There are a two key files that must be created for this to happen.

/etc/OpenBTS/OpenBTS.db

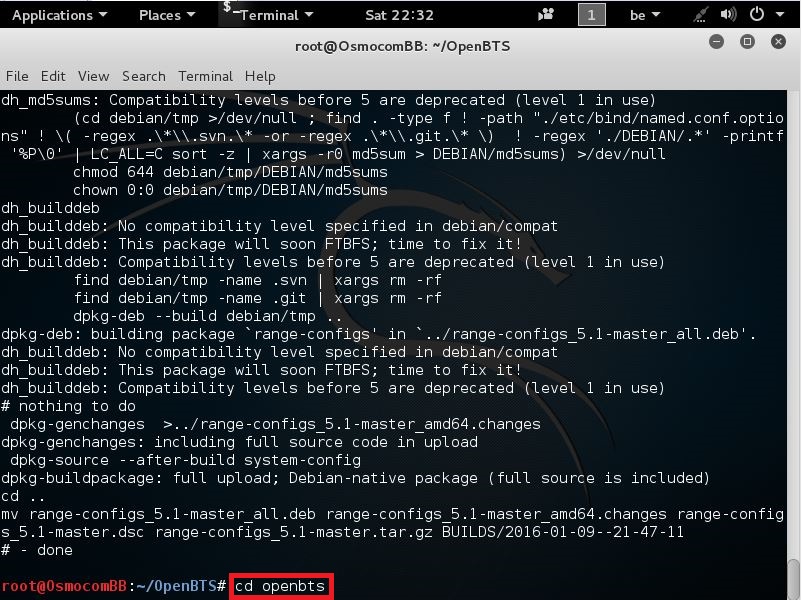
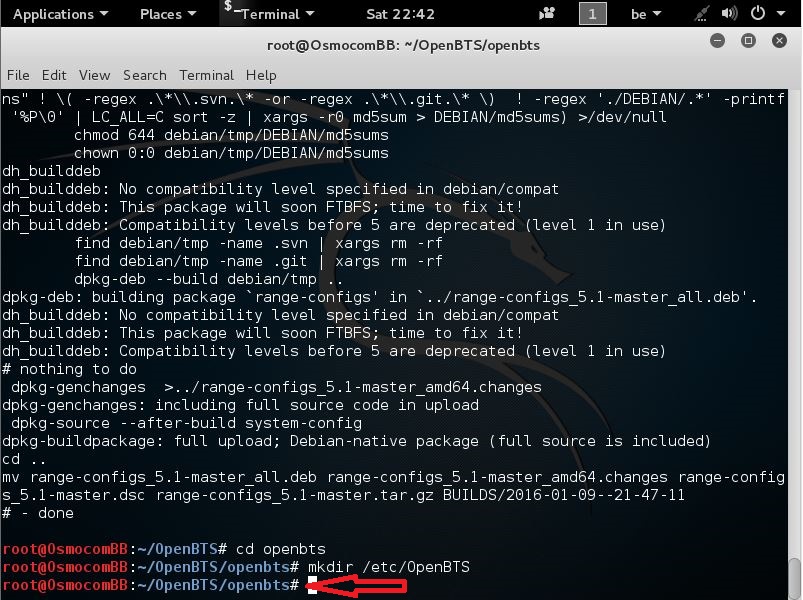
OpenBTS.db is the database store for all OpenBTS configuration. It must be installed at /etc/OpenBTS, which likely does not exist. So, to create this file, we first need to enter the OpenBTS directory

you do this by entering the following command

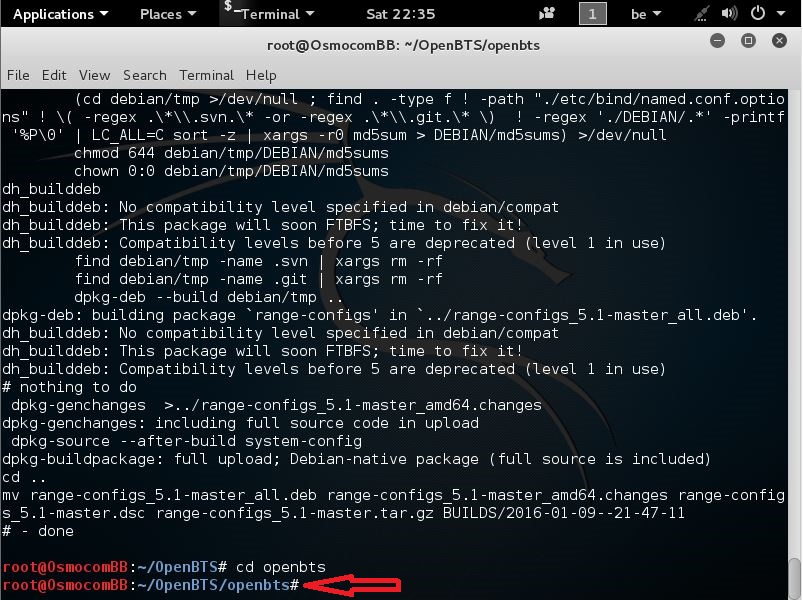
cd openbts

like seen here

now that this in entered u can press Enter

and should be here

now that u are in this location

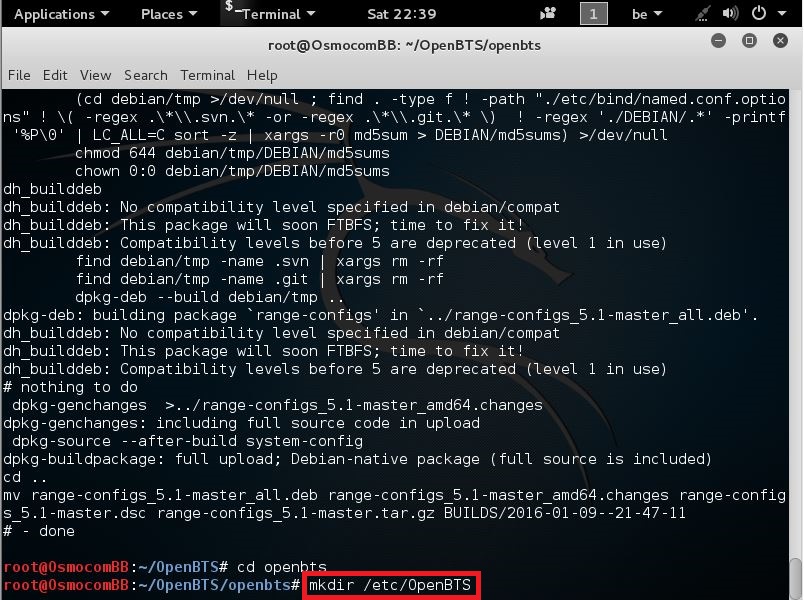
we are going to make a directory elsewhere, it’s the one we need for putting the database

so enter the following command:

mkdir /etc/OpenBTS

like seen here

now that u typed this command press Enter

You will see nothing happening but should come out back here again

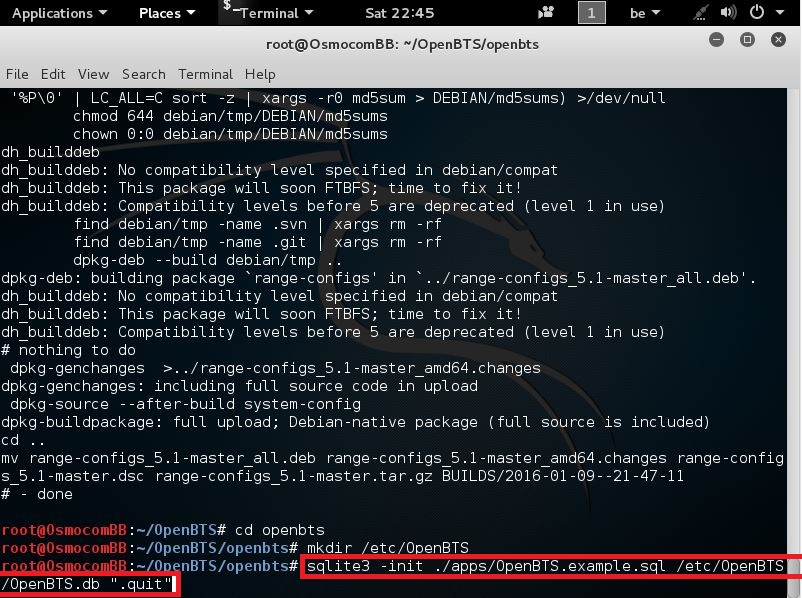
next we need to run the following command:

sqlite3 -init ./apps/OpenBTS.example.sql /etc/OpenBTS/OpenBTS.db ".quit"

like seen here

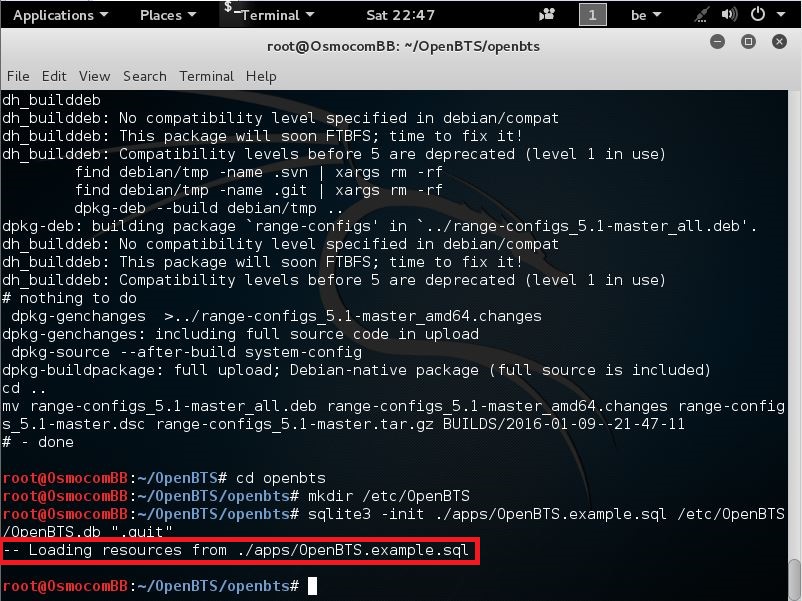
when u typed that command u can press Enter

and should see this

To make sure that it worked we are going to test it

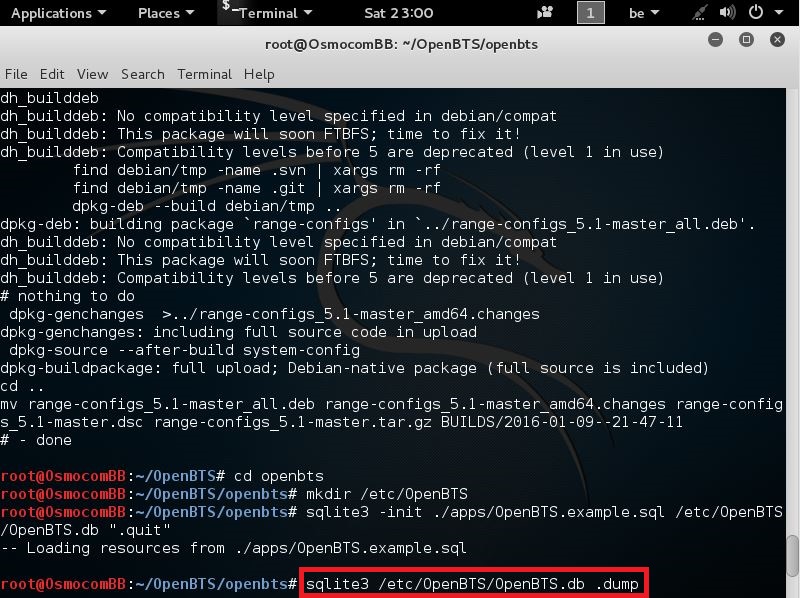
Test this by running the following command :

sqlite3 /etc/OpenBTS/OpenBTS.db .dump

like seen here

after u pasted that command press Enter

If you see a lot of configuration variables, the DB has been installed correctly.

so like this

this means that the database is configured correctly

At this point, we should be able to perform a basic sanity check of OpenBTS.

so we are going to do this

the openbts executable is in the apps folder

so we need to enter that by typing the following command here:

cd apps

like seen here

after that press Enter

and you should now be here

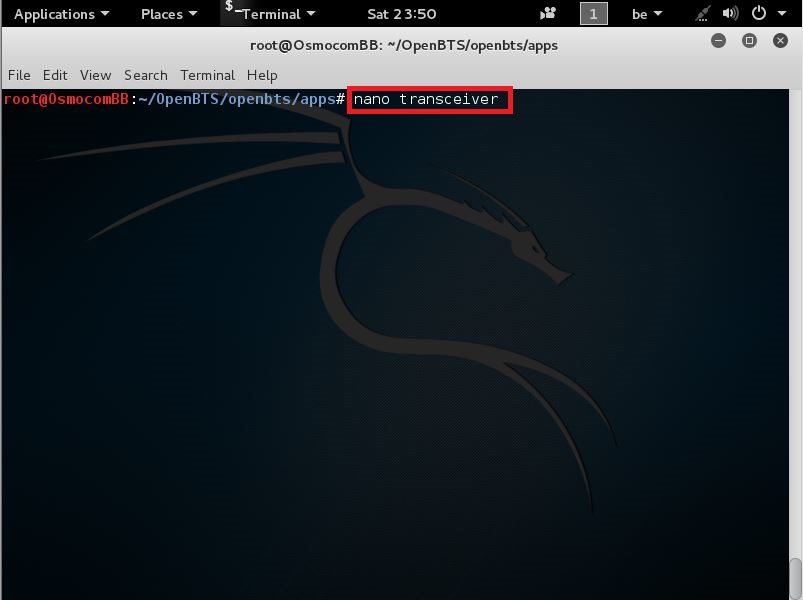
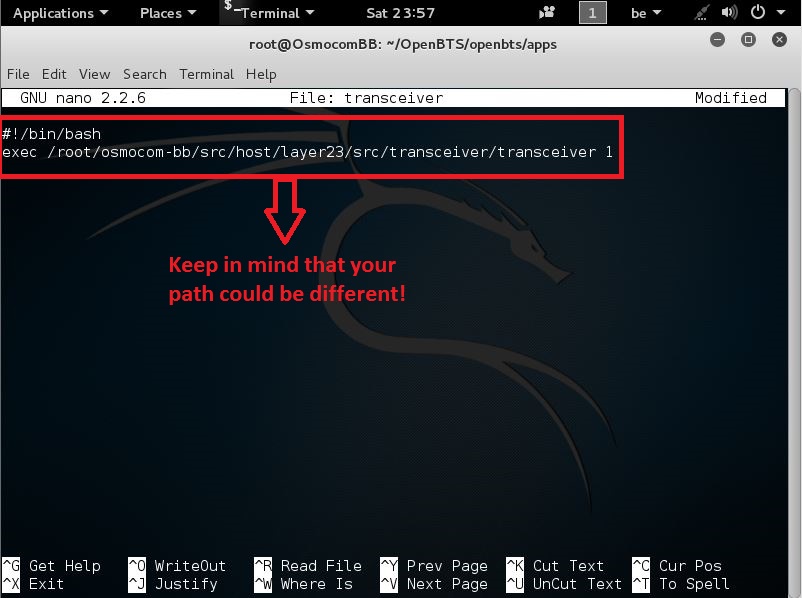
next we need to create a script with the filename transceiver with the following content and make it executable:

#!/bin/bash
exec <your path to osmocom-bb>/src/host/layer23/src/transceiver/transceiver 1

so to do that we need to type the following command:

nano transceiver

like seen here

when u typed out this u can press Enter

and should then see this

now that u have this open

we should paste the following lines here:

#!/bin/bash
exec /root/osmocom-bb/src/host/layer23/src/transceiver/transceiver 1

like seen here

If you followed all my guides, it should be correct..But if u installed osmocom-bb in another location u should change that here

Whereas 1 needs to be replaced with the ARFCN of the reference cell you want to use for synchronization

(find a strong one with the rssi-app for example).

But when that is done we can continue

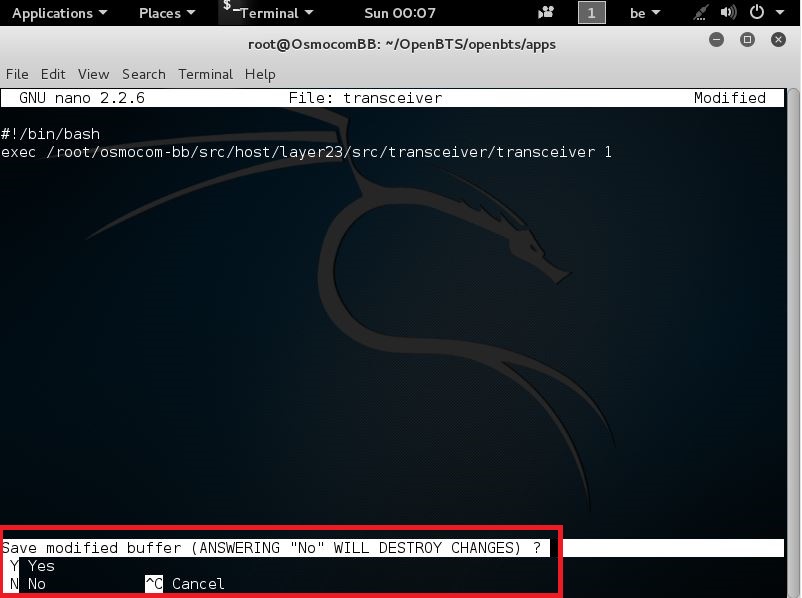
Press CTRL+X to close

and you should then see this

now that u see this u can press Y on your keyboard

and should then see this

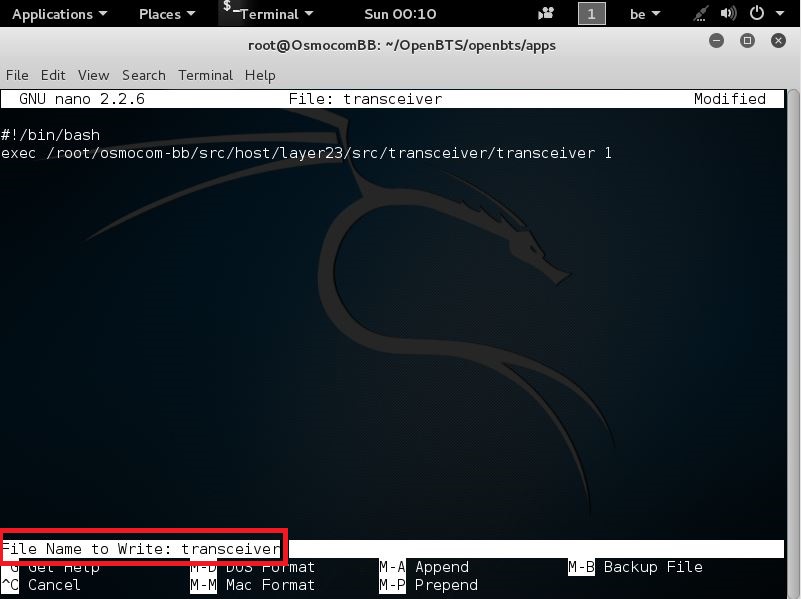
now when you see this u can just press Enter

and it should be saved now

And you should now come back out here again

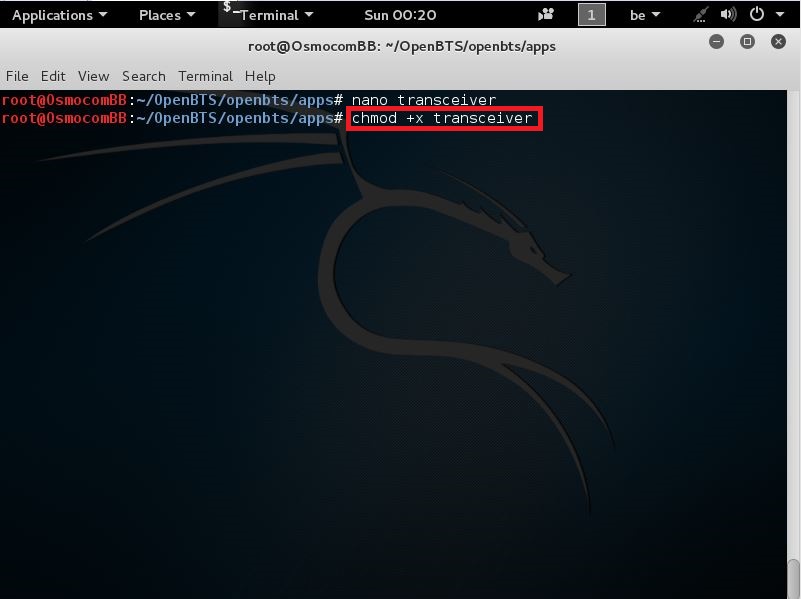
now that u are here again, we need to make the file we just created executable

we do this by running the following command:

chmod +x transceiver

like seen here

now that u typed this command, u can press Enter

You will see nothing happening but the file should be executable

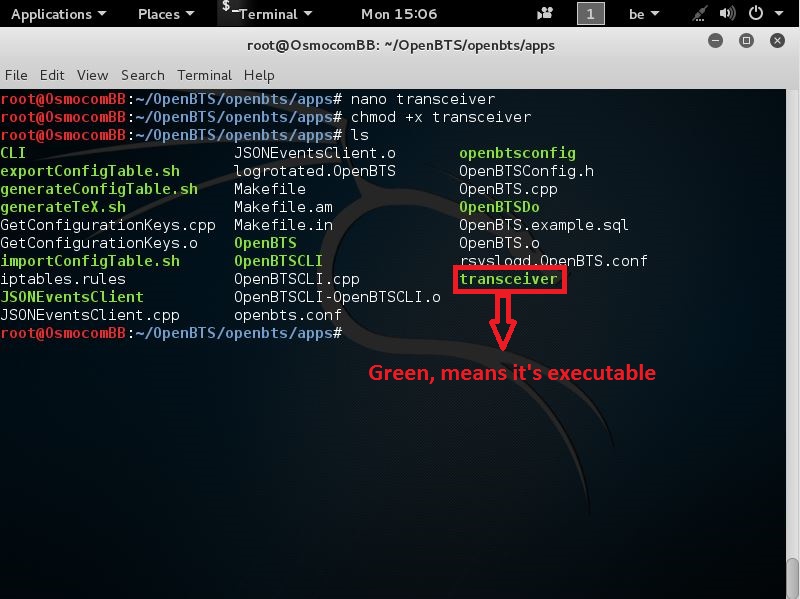
you can check this by running the following command:

ls

and should then see this

the file transceiver in green (which means it’s executable!)

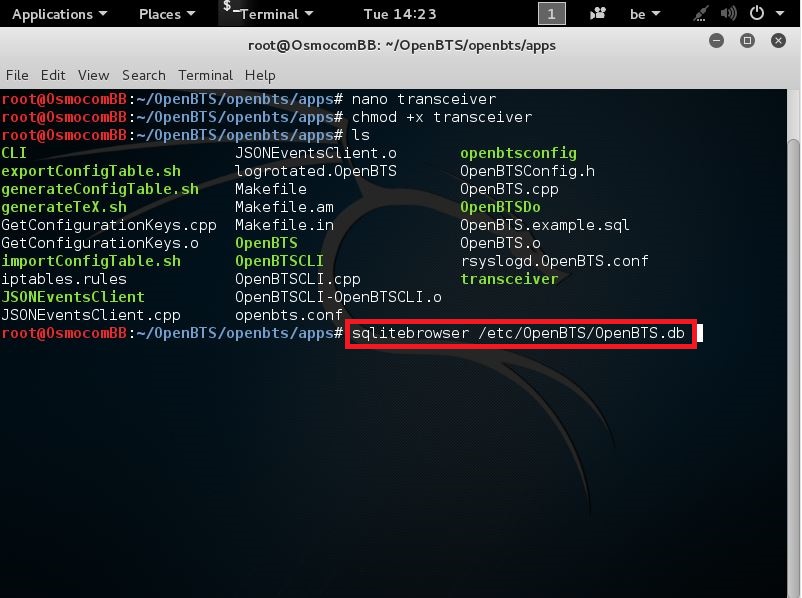
Now that this is done we need to make some changes to the OpenBTS database.

We do this by entering the following command:

sqlitebrowser /etc/OpenBTS/OpenBTS.db

like seen here

now that u entered that command press Enter

and should now see this

now that u see this we need to click on the Tab Browse Data

like seen here

when you clicked that, u should see this

now we need to make some changes here

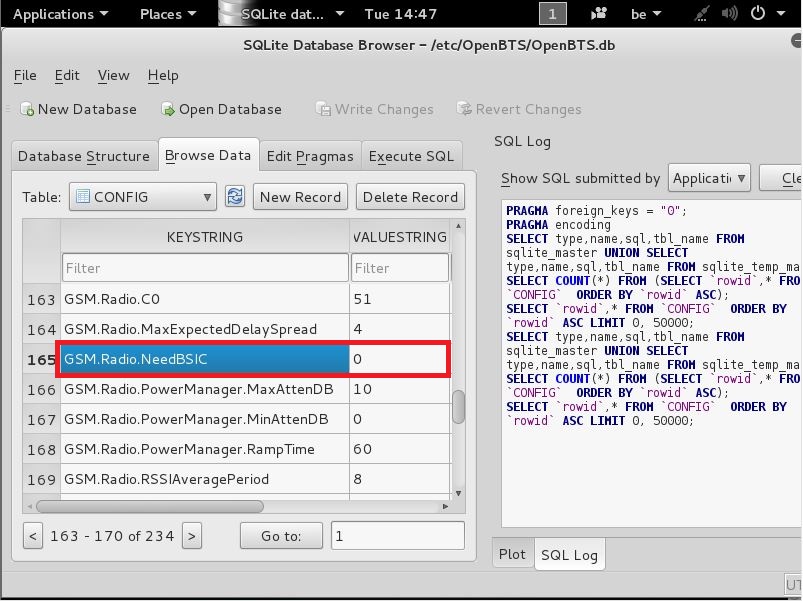
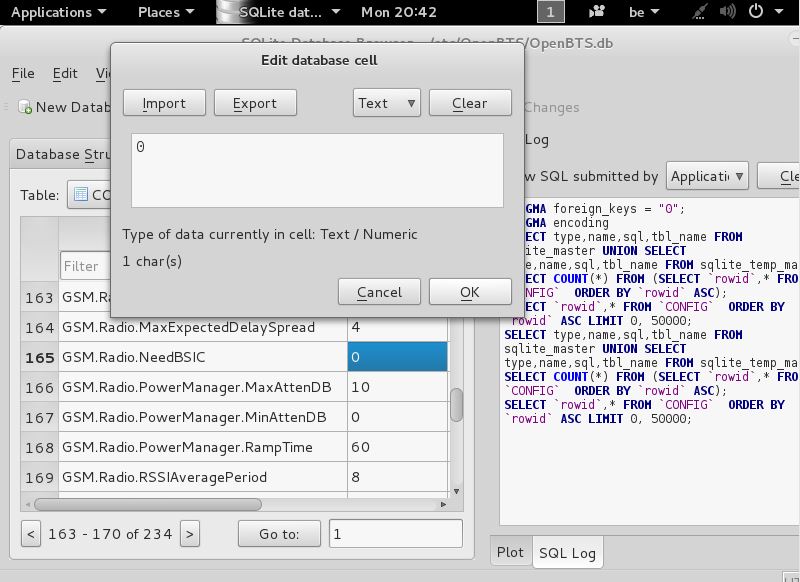
find the line

GSM.Radio.NeedBSIC

like seen here

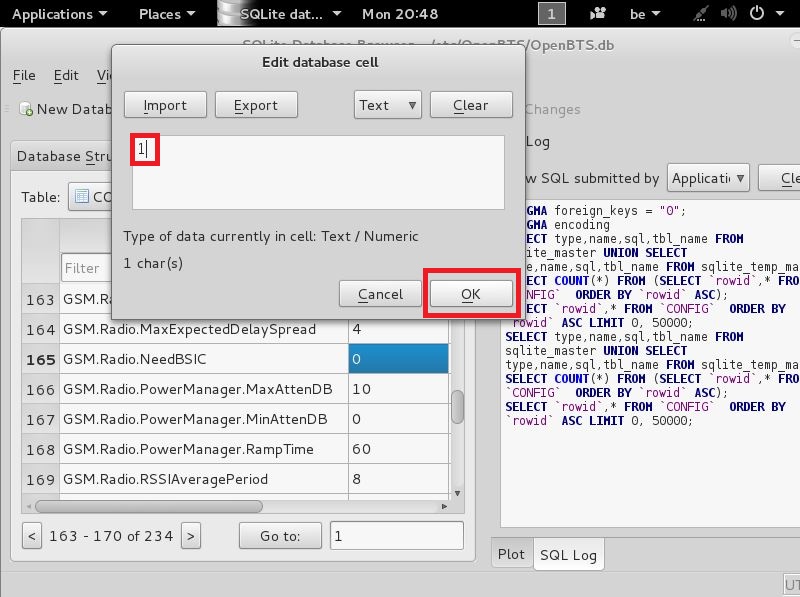
now that u see this double click on the 0 (zero) next to it

and you should then see this

when u have this edit window open

change the 0 (zero) to 1 (one)

like seen here

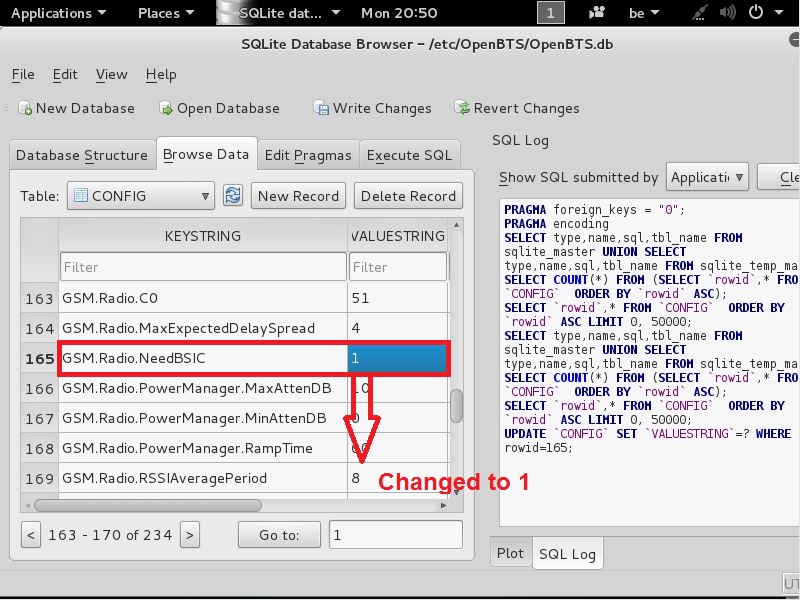
and then click OK

and should then come back out here again

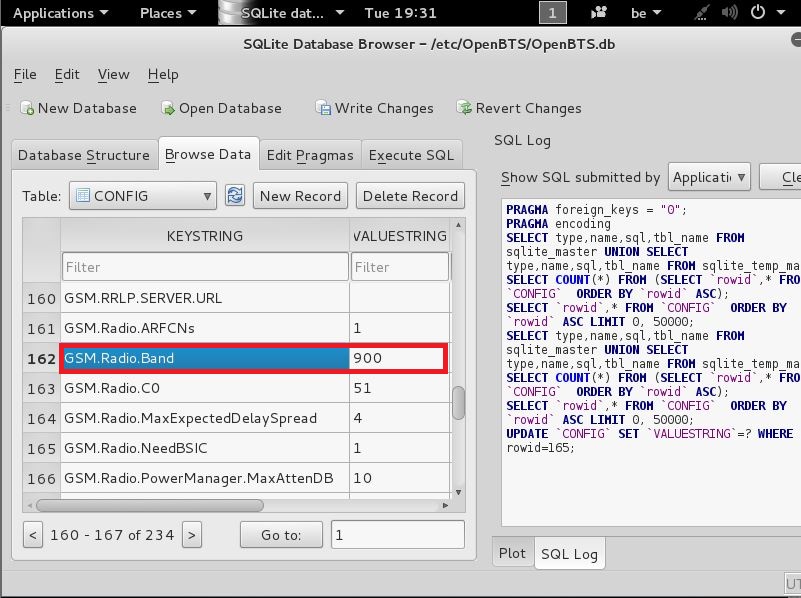
now that this is done find the following line

GSM.Radio.Band

like seen here

and make sure the VALUESTRING is set to 900

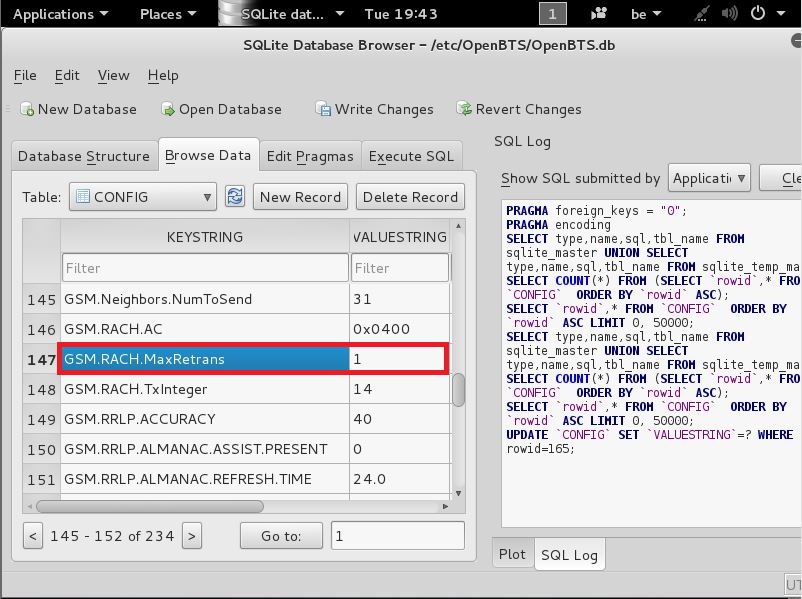
next look for the following line

GSM.RACH.MaxRetrans

like seen here 

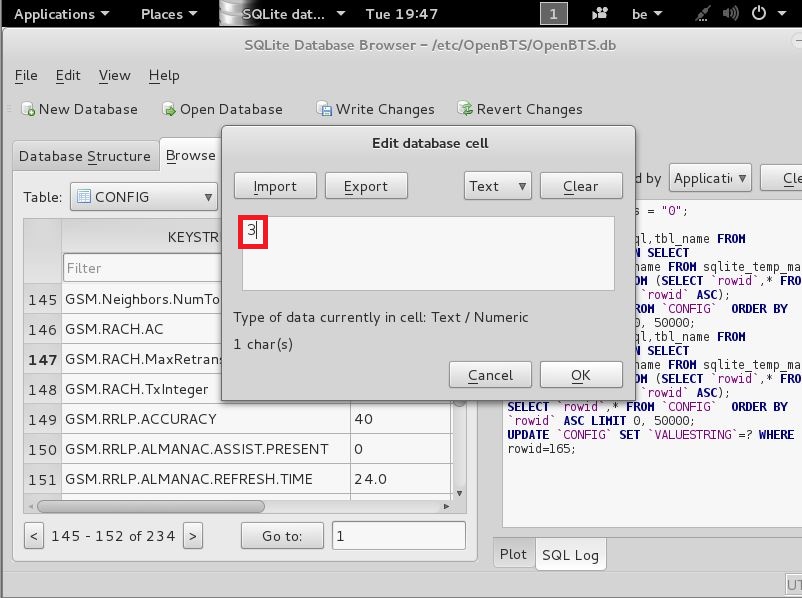
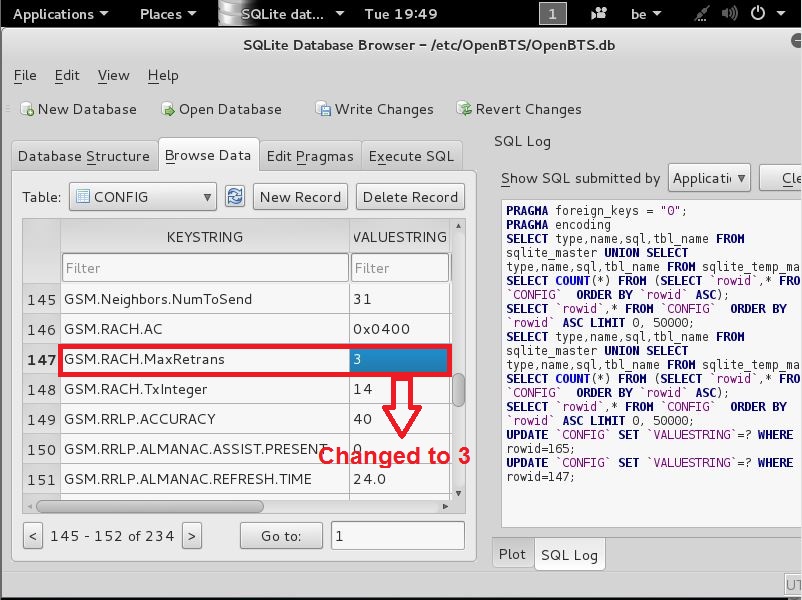
and change that VALUESTRING 1 to 3

like seen here

and then press OK

and you should then have this

now that this is done

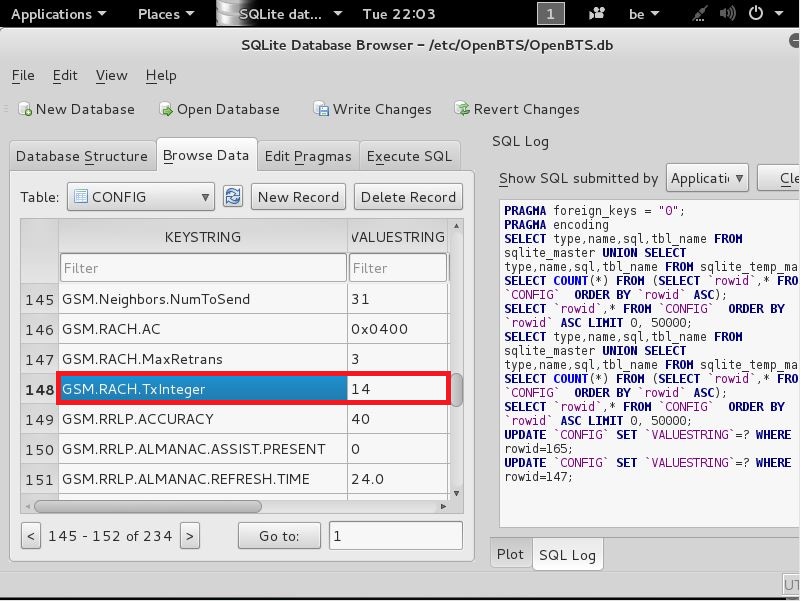
we need to look for the following line

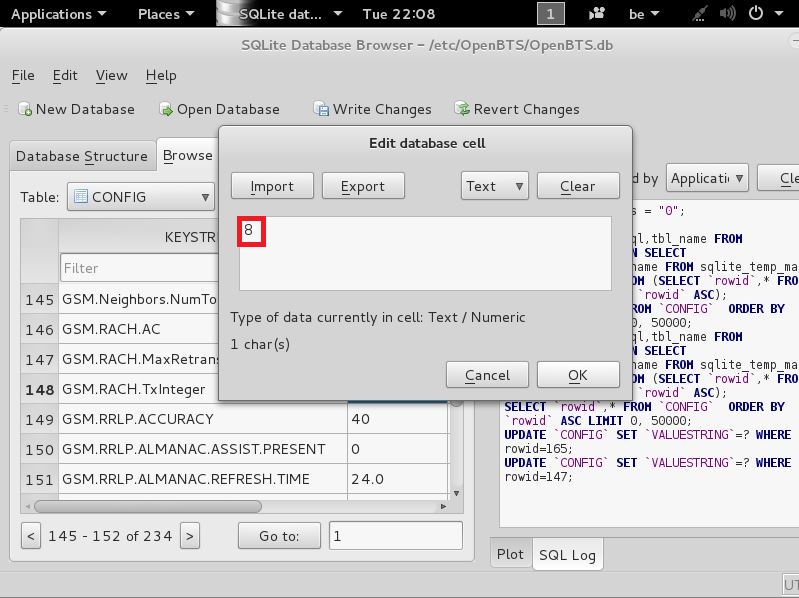
GSM.RACH.TxInteger

like seen here

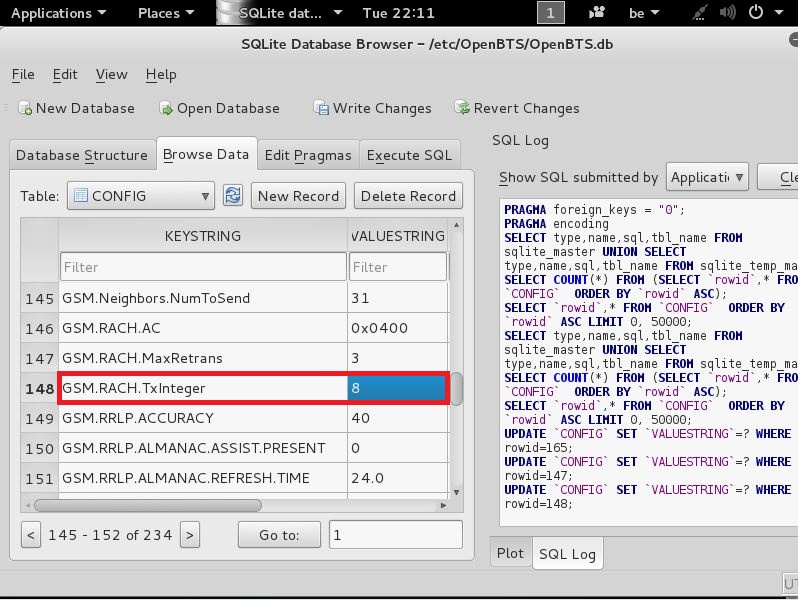
now that u found this change the VALUESTRING from 14 to 8

like seen here

now that this is done click on OK

and you should then have this